For coupled equations arising for A independently-moving bodies,
at total energy E we have to solve a set of N coupled
equations in a radial variable r
for channels labelled
![]() :
:
For two-body problems, r is the separation of the bodies and m is the
reduced mass, while for three- or more-body problems this equation arises
when r is the hyperradius ![]() , and m is a unit scaling mass.
, and m is a unit scaling mass.
The ![]() refers to a set of additional quantum numbers. For three-body
problems with inert particles and a spin-zero core,
refers to a set of additional quantum numbers. For three-body
problems with inert particles and a spin-zero core,
![]() ,
while in general the quantum numbers of the A interacting bodies will be included in the
set
,
while in general the quantum numbers of the A interacting bodies will be included in the
set ![]() .
.
We use the channel momenta
![]() .
The radial wave functions
.
The radial wave functions
![]() for bound states
then have the standard boundary conditions of
for bound states
then have the standard boundary conditions of
Here
![]() and
and
![]() are the Coulomb functions of
index
are the Coulomb functions of
index ![]() , with asymptotics
, with asymptotics
![]() describing the in- and out-going spherical waves. The appropriate value of the Coulomb
parameter
describing the in- and out-going spherical waves. The appropriate value of the Coulomb
parameter ![]() is given in section 2.5.
The Sij is the S-matrix for the outgoing amplitude in channel i from
an incoming plane wave in channel j.
We only deal with Borromean or democratic types of many-body problems,
so we do not treat explicitly any sub-system bound states in the asymptotic regions.
is given in section 2.5.
The Sij is the S-matrix for the outgoing amplitude in channel i from
an incoming plane wave in channel j.
We only deal with Borromean or democratic types of many-body problems,
so we do not treat explicitly any sub-system bound states in the asymptotic regions.
Note that for zero potentials S=1, and the scattering wave functions become
| (4) |
The wave functions of the coupled problem (1) can now be
solved completely over the interior range [0,rm], by using the
orthonormal basis set of the
{fqi(r)}
with coefficients to be determined. The coefficients are found in two stages:
first by finding all the eigensolutions ![]() of the
equations (1) using the above orthonormal basis, and then
expanding the scattering wave functions in terms of these
of the
equations (1) using the above orthonormal basis, and then
expanding the scattering wave functions in terms of these ![]() .
.
The first stage, the diagonalisation of interior Schrödinger equation (1)
yields P=QN eigenenergies ep with corresponding multichannel eigenstates
For scattering states at arbitrary energy E, the coupled
solutions are then expanded in terms of the multichannel eigenstates as
| (7) |
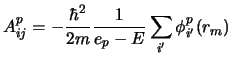 |
|||
| - | (11) |
The coefficients cpqi and energies ep in eqn.
(6) satisfy matrix equations
| (15) |
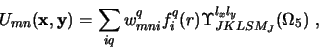 |
(17) |
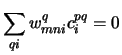 |
(18) |
We now diagonalise in the allowed subspace of P c = 0,
and ensure this by replacing matrix equations (13) by
The radial wavefunction describing the scattering with
in the outer region of configuration space,
where exchange effects and orthogonality conditions may be neglected,
satisfies the set of coupled differential equations Eq. (1),
which we now write as
Beyond a certain radius, the coupling interactions
Vii' in addition to the Coulomb potential
are assumed to be extrapolated by means of a multipole expansion
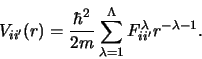 |
(22) |
R-matrix propagator techniques have been widely used to integrate the equations describing atomic and molecular scattering problems. In essence the radial interval over which the equations are to be integrated is divided into sectors. The known R-matrix on one boundary of a sector is then used to obtain the R-matrix on the other. The process is continued so that the R-matrix is moved from one extreme of the interval of interest to the other. The principal advantage of this approach over alternative methods is very high numerical stability. A second important feature is that propagator methods are very economic in cases where large numbers of scattering energies must be considered. Much of the calculation which must be carried out within a given sector may be saved for energies subsequent to the first by saving appropriate sector information.
Equations (21) may be rewritten for a given solution, j, as
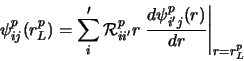 |
(24) |
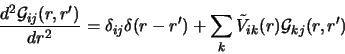 |
(25) |
Various propagator methods exist which differ on how the the sector Green's functions are determined. As the present package is designed to treat scattering in a region outside the range where the interaction potential is slowly varying, a potential following approach should be in general the most appropriate. The primary propagator method used is therefore one proposed by Light and Walker [12], [13], [14] which assumes that the interaction potential is constant within each sector. With this choice the sector Green's function matrices are rapid to compute and accuracy is maintained by varying the sector size. In practice it is found that sector sizes may become extremely large so this choice provides enormous computational advantages over solution-following methods.
In the Light-Walker (LW) approach the interaction potential is
diagonalized at the centre of each sector. This defines an
orthogonal transformation which may be used to decouple the
Green's function equations within the sector. Therefore for the
p-th sector centred at r=rCp if
| (28) |
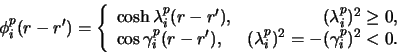 |
(30) |
The sector size is determined by estimating the error
resulting from variations in the potential over a sector.
For example, the size of the (p+1)-th sector, Lp+1, is given by
![\begin{displaymath}
\beta\left [ \left \{ 2\sum_{i=1}^N\frac{(\lambda_i^p)^2-(\l...
...p-1})^2}
{N(L^p+L^{p-1})} \right \}^2 \right ]^{-\frac{1}{6}}.
\end{displaymath}](img77.gif) |
(31) |
As discussed in Stechel et al [13] channels which do not contribute to the scattering can be dropped during propagation by simply truncating the R-matrix between one sector and the next. Such channels are deeply bound with slight coupling with open and less deeply bound channels. An estimate of the coupling of a channel j with channels (1,2,...,j-1) is given by the quantity qpj where
| (33) |
The radial scattering equations must be integrated outwards from the boundary of the R-matrix internal region to a point where they can be matched to the asymptotic form of the solution with the appropriate boundary conditions. This integration region can be greatly reduced (and sometimes eliminated) by obtaining and matching to the solution of the scattering equations obtained analytically in the form of an asymptotic series which can be summed by the application of series acceleration techniques. In the present program an asymptotic series suggested by Gailitis[15] is summed using a simplified version of the Padé algorithm used by Noble and Nesbet [16]. The expansion selected has a number of advantages. First, a large part of any residual Coulomb interaction is removed from the asymptotic expansion and the recursion relation used to calculate the expansion coefficients contains terms which depend on the factor Z/k rather than on (Z/k)2. Second, the expansion may be determined directly from a single set of recursion relations rather than indirectly by expanding and dividing out the Coulomb factors. Finally, the expansion is conveniently expressed in a form which is highly vectorizable provided the number of scattering channels is large.
Assume that a solution of each component of equations (21) may be written in the form
| (36) |
Substituting the expansion given by equation (34) into equation (21)
yields recursion relations for
the expansion coefficients
![]() and
and
![]() of the form
(assuming Z = Zi)
of the form
(assuming Z = Zi)
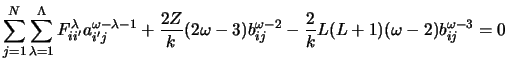 |
(37) |
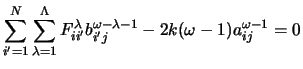 |
(38) |
The required 2N open-channel solutions are found by choosing k2 = ki2 for
![]() and taking the regular Coulomb solution
and taking the regular Coulomb solution
![]() for
solutions corresponding to the boundary condition
for
solutions corresponding to the boundary condition
and the irregular solution
![]() for the boundary condition
for the boundary condition
where
| (41) |
| (42) |
The coefficients aij0, bij0 are arbitrary if ki2 = k2
or zero if
![]() .
We therefore assume that
.
We therefore assume that
![]() and bij0 = 0 so that
and bij0 = 0 so that
| (43) |
In the case of closed channels, ki2 < 0, the solution R is taken equal to
R(r) = H+(kir). Also
![]() and
and
![]() .
With this choice the closed channel solutions asymptotically
assume the usual form of Whittaker functions since
.
With this choice the closed channel solutions asymptotically
assume the usual form of Whittaker functions since
| (44) |
If we replace ![]() by
by ![]() in the previous equations,
the recursion relations for both open and closed channels may be expressed as
in the previous equations,
the recursion relations for both open and closed channels may be expressed as
Given the expansion coefficients obtained from eqs (45-48) the solutions are defined by Eq. (34). The traditional methods for evaluating asymptotic series of this form are able to provide accurate solutions only at large radial distances r. Noble and Nesbet [16] have shown that series acceleration techniques may be used to evaluate the wavefunctions and their derivatives at much smaller radial distances. In the present package a simplified version of the algorithm used by Noble and Nesbet is employed.
An important feature of the approach we have adopted is that, given the coefficients of the asymptotic expansion, the wavefunctions and their derivative may be determined rapidly at a series of radial points in order to determine the minimum distance necessary to achieve the required level of accuracy. The accuracy of the results obtained is determined from the computed value of the multichannel Wronskian relations [17].
If all N scattering channels are open the asymptotic form of the radial
wavefunction describing the scattering
may be written in the form
It is necessary to match the R-matrix
obtained by outwards propagation from the internal region boundary to the
asymptotic radial solutions obtained using the techniques described in the
previous subsection. Given the asymptotic form of the radial wavefunctions defined
by Eq. (49) it follows that the real symmetric K-matrix, K, is given by
| (50) |