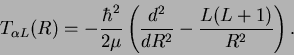We consider the scattering of a projectile a by a target A.
We denote this partition by the index ![]() , i.e.,
, i.e., ![]() .
The Hamiltonian of the system is expressed as:
.
The Hamiltonian of the system is expressed as:
| (9) |
We assume for simplicity that only one of the nucleus (let's say,
a) is excited during the collision and that this nucleus has only
one excited state. The model wavefunction will have both elastic and
inelastic components. It can be expressed as [3]:
| = | |||
| = | (11) |
The functions
![]() and
and
![]() describe
the relative motion between the projectile and target in the different
internal states. The total wavefunction
describe
the relative motion between the projectile and target in the different
internal states. The total wavefunction ![]() verifies the Schroedinger
equation:
verifies the Schroedinger
equation: ![]() . By projecting this equation onto the different
internal states a set of two equations is obtained:
. By projecting this equation onto the different
internal states a set of two equations is obtained:
If the number of states is large, the solution of the coupled equations
can be a time consuming task. In many situations, however, some of
the excited states are very weakly coupled to the ground state. For
example, referring again to the two channels case, this suggests that
the inelastic component of the total wavefunction (10)
is going to be a small fraction of the elastic one. This allows to
get an approximated solution of the coupled equations by setting to
zero the inelastic component in the first equation:
Thus, the first equation can readily solved. The resulting function
![]() ) is then inserted into the second equation,
allowing the calculation of
) is then inserted into the second equation,
allowing the calculation of
![]() . This is called 1-step
distorted wave distorted wave Born approximation (DWBA). An iterative
procedure can be then applied by inserting the calculated
. This is called 1-step
distorted wave distorted wave Born approximation (DWBA). An iterative
procedure can be then applied by inserting the calculated
![]() into the first equation in (12) to get an improved function
into the first equation in (12) to get an improved function
![]() . Continuing this procedure, we can get 2-step, 3-step,
etc DWBA. When the couplings between channels are weak, the DWBA should
approach to the full CC solution. However, when couplings are strong
convergence problems can be presented.
. Continuing this procedure, we can get 2-step, 3-step,
etc DWBA. When the couplings between channels are weak, the DWBA should
approach to the full CC solution. However, when couplings are strong
convergence problems can be presented.
As in the pure OM calculation, a separation between the angular and
radial parts is made in the set of coupled equations (12).
This requires the expansion of the potentials
![]() and
and
![]() in multipoles. For example:
in multipoles. For example:
The resolution of the coupled equations (12) is significantly
simplified if the distorted wavefunctions are separated into their
radial (![]() ) and angular parts. Thus, inserting the multipole
expansion (14) into the coupled set of equations one
gets:
) and angular parts. Thus, inserting the multipole
expansion (14) into the coupled set of equations one
gets: