3.2.0.2 Coulomb deformation:

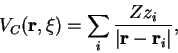
The Coulomb potential between a charge Z and a distribution of charges z_i is

$$V_{C}(\mathbf{r},\xi)=\sum_{i}\frac{Zz_{i}}{\vert\mathbf{r}-\mathbf{r}_{i}\vert},$$

with $\xi=\{\mathbf{r}_{i}\}$

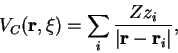
Again, this potential is expanded in multipoles, resulting

$$V_{C}^{\lambda\mu}(R,\xi)=M(E_{\lambda\mu})\frac{\sqrt{4\pi}e^{2}}{2\lambda+1}\frac{Z}{R^{\lambda+1}},$$

where

$$M(E_{\lambda\mu})=\sum_{i}z_{i}r_{i}^{\lambda}Y_{\lambda\mu}(\hat{r}_{i})$$

is the multipole electric operator.

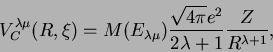
In this scheme, the coupling potentials U_ij are the matrix elements of the operator $V_{C}^{\lambda\mu}(R)$ between different excited states. In the collective model, these states are characterized by their angular momentum I and projection M. Using the Wignet-Eckart theorem

$$\langle I'M'\vert V_{C}^{\lambda\mu}\vert IM\rangle=(2I'+1)^... ...\rangle\langle I'\vert\vert V_{C}^{\lambda}\vert\vert I\rangle,$$ (21)

where $\langle IM\lambda\mu\vert I'M'\rangle$ is just a Clebsch-Gordan coefficient and $\langle I'\vert\vert V_{C}^{\lambda}\vert\vert I\rangle$ is the so called reduced matrix element for the operator $V_{C}^{\lambda}$. These are given by:

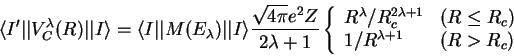$$\langle I'\vert\vert V_{C}^{\lambda}(R)\vert\vert I\rangle=\... ... (R\leq R_{c})\\ 1/R^{\lambda+1} & (R>R_{c})\end{array}\right.$$ (22)

The evaluation of $\langle I'\vert\vert M(E_{\lambda\mu})\vert\vert I\rangle$ depends on the model used. We consider two cases:

• Rotational model:
  

  $$\langle I'\vert\vert M(E_{\lambda})\vert\vert I\rangle=\sqrt... ...rt I'K\rangle\langle\chi\vert M(E_{\lambda0})\vert\chi\rangle,$$ (23)

  
  
  where K is the rotational band and $\langle\chi\vert M(E_{\lambda0})\vert\chi\rangle\equiv M_{n}(E\lambda)$ is the expected value of the electric operator $M(E_{\lambda0})$ in the intrinsic state of the deformed nucleus. The only information required by FRESCO are the expentation values $\langle\chi\vert M(E_{\lambda0})\vert\chi\rangle$, which are assigned to the variables $P(\lambda)$:
  

  $$P(\lambda)=\langle\chi\vert M(E_{\lambda0})\vert\chi\rangle$$ (24)

  
  

• Experimentally, $\langle I'\vert\vert M(E_{\lambda\mu})\vert\vert I\rangle$ can be directly related to the reduced transition probability $B(E\lambda;I\rightarrow I')$:
  

  $$B(E\lambda;I\rightarrow I')=\frac{1}{2I+1}\vert\langle I'\vert\vert M(E\lambda)\vert\vert I\rangle\vert^{2},$$ (25)

  
  
  for the off-diagonal matrix elements. For quadrupole deformations, the diagonal matrix elements are related to the experimental quadrupole moment by:
  

  $$Q_{2}=\sqrt{\frac{16\pi}{5}}(2I+1)^{-1/2}\langle II20\vert II\rangle\langle I\vert\vert M(E_{2})\vert\vert I\rangle,$$ (26)

  
  
  for the diagonal reduced matrix elements. Each matrix element is provided in a separated &step/ namelist.
  - ib: final state with angular momentum I'
  - ia: initial state with angular momentum I
  - k: multipolarity $\lambda$
  - str: strength of the coupling factor
  

  $$STR=M(E\lambda)=(-1)^{\frac{I-I'+\vert I-I'\vert}{2}}\langle... ...vert\vert I\rangle=\pm\sqrt{(2I+1)B(E\lambda;I\rightarrow I')}$$ (27)

  
  

Table 1: Information required by FRESCO to construct the coupling potentials in a CC calculation

Coupling

TYPE

P(k)

STR Coulomb: rotational